What if I told you that humans have been simulating tiny universes on computers? They're not quite the size of our universe, or even of something smaller like a planet. They're only about 10 femtometers across, smaller than an atom. But it's a start.
They're called Lattice simulations, and belong to a subgenre of particle physics called Lattice Gauge Theory.
To illustrate what this is and why it matters, let's consider a very simple and general physics problem: working out the trajectory of an electron. Deducing a trajectory is to be able to say where the electron is at any given point in time.
In classical mechanics (how the world looked before the early 20th century, when quantum theory turned everything on its head ), the trajectory can be deduced with certainty. Consider, for example, an electron moving through a magnetic field. Given the strength of the magnetic force acting on the electron, along with the initial conditions, like its position and velocity, there exists a single, unique trajectory a particle can take. If you plug these initial conditions into an equation of motion (like Newton's 2nd law, by which the force of an object equals its mass multiplied by its acceleration), you can solve it to deduce the position of that particle after some arbitrary period of time.
If you take quantum mechanics into account, things get a little more complex. The electron is no longer bound to follow this unique trajectory, but can take other trajectories which disobey its classical equation of motion. According to Classical Mechanics, the probability of the electron following the classical path was 1, and following any other path was 0. Now, every path has a non-zero probability, which falls somewhere between 0 and 1.
Now, no one can predict with certainty where the particle will be after a period of time. However, it is possible to determine the probability of the particle arriving at a certain point in space at a given time.
To calculate this, a quantum physicist would basically add up the probabilities of each of the many trajectories that result in the electron arriving at your chosen location at your chosen time. This is called a path integral, the sum of all probabilities of a particle taking each possible path between two points. There are an infinite number of possible paths. The classical path is always the most likely, paths that are close to the classical path have a smaller probability but still contribute, and completely deviant paths have a negligible effect.
One of the reasons quantum mechanics is 'hidden' at sizes bigger than an atom is that the deviant paths become so unlikely that the classical path is basically the only path the particle can take.
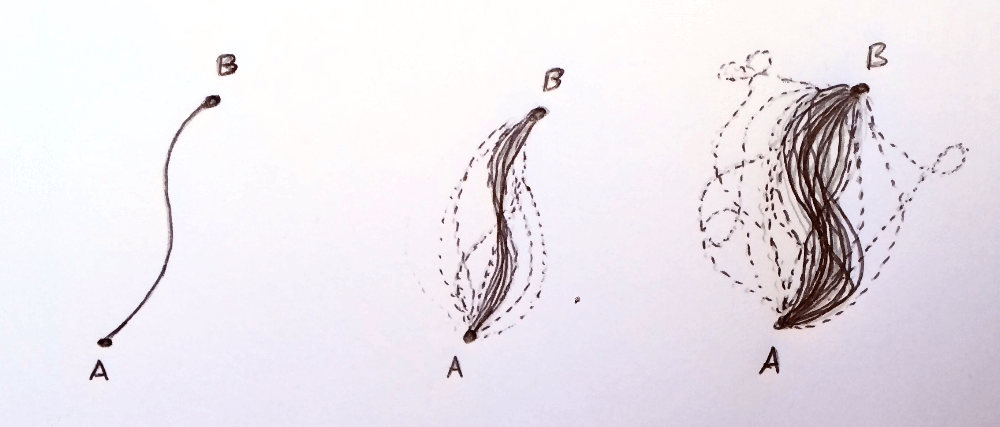1. Particle travelling from A to B. Rightmost- a particle, e.g. an electron, on the quantum scale. Leftmost- a particle, e.g. a baseball, on the classical scale. Solid lines are "very likely paths", and dotted are less likely
Now let's complicate the picture further by moving from quantum mechanics to quantum field theory, the language we use to express theories of the bare bones of the universe. This takes into account the possibility of the electron emitting and absorbing particles, or decaying into different particles only to reappear somewhere down the line before reaching its destination. Things become more complicated, but the principle of the path integral still holds, except now the bunch of paths we need to add up now include all combinations of emissions and decays. I'll refer to a 'path' as a specific trajectory along with any specific interaction with other particles.
2. Similar to figure 1, now with the possibility of other particles being created and destroyed
As you can see, once we're in quantum field theory, we are getting into some real fundamental shit.
In practice, it's not possible to work out probabilities for an infinite number of paths. As I previously discussed, there are a small number of dominant paths which account for the majority of the probability, such as the classical path and small perturbations of it. In particle physics, the way we usually work out the probability of a process like this is to consider only these dominant paths, and we get to a result which is pretty close to the 'true' answer. This is analytically tractable. In other words; it can be done with just a pen, paper and the knowhow. The method is referred to as perturbation theory.
Of course, this doesn't work for everything, and wouldn’t hold up if we were trying to compute the path integral for a quark rather than an electron. Electrons interact mostly with electromagnetic force (electricity+magnetism). Quarks feel not only the electromagnetic force, but also the strong nuclear force, making them horrendously more complicated. The strong force is 'purely quantum' in the sense that there isn't really a single dominant path or various subdominant perturbations of the path. Instead, there are many different dominant paths and there is no good way to order them in terms of probability.
It's possible to use perturbation theory on quarks, but since it's difficult to find all the dominant paths, uncertainties usually lie at around 10%. Compare this with what one can achieve with the electron, with uncertainties dipping well below 1%.
The solution: lattice simulations! (Remember those?)
Simulate a small period of time playing out on a small patch of space on a powerful computer, give the patch a little prod so it has enough energy for a quark to appear, and let your tiny universe play out all the possible paths, decays, interactions, whatever.
Inside the patch it's necessary to approximate space and time as a lattice of individual points. Each point has some numbers attached to it, signifying the probability of a quark being at that point, the probability of the presence of other quarks, and the strength of the strong force. With this little universe, we can forget about which paths are dominant and which aren't, since all paths occur automatically in the simulation.
3. A two-dimensional lattice
Like perturbation theory, this too is an approximation. As far as we know, Spacetime is not discrete: in reality, there are an infinite number of possible positions in space and moments in time. So ... physicists will often perform the simulation at many different 'lattice spacings' (the width of gaps between points), study how the results change when lattice spacing changes, and from that work out what the answer would be on a continuous spacetime, one that takes into account the infinite number of possible divisions. Similarly, in the real world, there are no 'walls' like there are on the edges of the patch. So folks will use a range of sizes of patch, and extrapolate results to an infinite size where there are no walls.
Uncertainties in lattice simulations are in many cases a lot smaller than perturbation theory, at about the 1% level. The method has proven amazingly effective in understanding how quarks bind together to form mesons. A meson is like the little brother of the proton and neutron: while these contain 3 bound quarks, a meson contains 2. Lattice people have their sights on making a simulation big enough that a whole proton can fit inside its walls, but we're not quite there yet.
I think lattice gauge theory is still only in its 'calibration phase' - like a new instrument that needs tuning. Currently, most of the work done consists of matching predictions to experiments. However, our computers are becoming faster, our methods more efficient, and our understanding of the physics is improving. By simulating spacetime, the lattice could end up being the number one method of choice for making predictions in particle physics. Watch this space.